
As with all calculations care must be taken to keep consistent units throughout. A moment of inertia is required to calculate the Section Modulus of any cross-section which is further required for calculating the bending stress of a beam. The Critical Axial load, Pcr is given as P cr 2 EI/L 2. The above formulas may be used with both imperial and metric units. The moment of inertia I is a very important term in the calculation of Critical load in Euler’s buckling equation. moment of inertia, centroids, cross section area and polar moment of inertia. The dimension of the moment of area is L 3, the SI units are m. However, for typical cross-sections, formulas can be used to calculate the moment of inertia. I know that I can calculate the moment of inertia of a rectangular cross section around a given axis located on its centroid by the following formulas: I also know that more generically, the moment of inertia is given by the integer of an area times the square of the distance from its centroid to the axis. plane (as is the case for the cross section of a beam), the rst moments of area with respect to the two axes are given respectively by: Z Z Q 2 x 3 dA Q 3 x 2 dA A A They are a measure of the distribution of the area of the shape with respect to the given axes. The following table, lists the main formulas, related to the mechanical properties of the I/H section (also called double-tee section).Notation and Units Metric and Imperial Units calculator, moment of inertia calculator, truss calculator, and more Canadian. The moment of inertia is calculated using the formula I mr2, where m is the mass of an object and r is the distance from the centroid of the mass to the axis of rotation. The I-section, would have considerably higher radius of gyration, particularly around its x-x axis, because much of its cross-sectional area is located far from the centroid, at the two flanges. Circle is the shape with minimum radius of gyration, compared to any other section with the same area A. It is a mathematical property of a section concerned with a surface area and how that area is distributed about the reference axis (axis of interest).

Beams - Fixed at Both Ends - Continuous and Point Loads Stress, deflections and supporting loads. Beam Loads - Support Force Calculator Calculate beam load and supporting forces. It is always considered with respect to a reference axis such as X-X or Y-Y. Area Moment of Inertia - Typical Cross Sections II Area Moment of Inertia, Moment of Inertia for an Area or Second Moment of Area for typical cross section profiles. im trying to avoid buying a new motor by replacing the hollow cylindrical beam with a triangular warren truss. ive got a canti-levered beam which is too heavy for the motor im using to rotate it. It is the special area used in calculating stress in a beam cross-section during BENDING. This equation is for a solid square where its centre of mass is along the x-axis. For each axis (x-x and y-y) exists one moments of inertia (Ixx and Iyy) and as the distance to the outer fibre is different in angle position (a) and (b) there. The Moment of Inertia (I) is a term used to describe the capacity of a cross-section to resist bending. my handbook of formulas has a myriad of entries for the moment of inertia of cross sections of various shapes. This engineering calculator will determine the section modulus for the given cross-section.
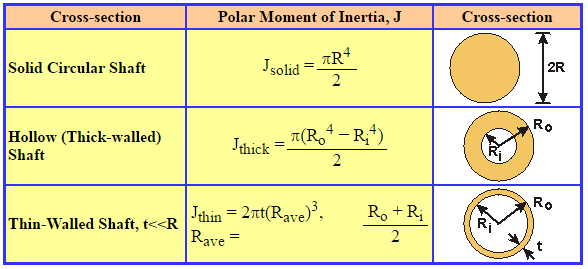
Small radius indicates a more compact cross-section. The moment of inertia of a square is given by the formula. Area Moment of Inertia Section Properties of Octagon Feature Calculator and Equations.
It describes how far from centroid the area is distributed. The dimensions of radius of gyration are. The moment of inertia of the cross-section (you can 1. Where I the moment of inertia of the cross-section about the same axis and A its area. The Maximum bending stress for circular section given moment of load formula is. Radius of gyration R_g of a cross-section, relative to an axis, is given by the formula: The area A and the perimeter P, of an I/H cross-section, can be found with the next formulas:


 0 kommentar(er)
0 kommentar(er)
